# Decomposition API
This post was originally part of the Making Speckle 2.0 series of posts on the community forum, it's been adapted as part of our dev docs. Check out the original on our forum (opens new window)!
# Preamble
This page covers how Speckle deals with the structure and composition of design data. Please note that currently examples are only in C#, equivalent implementations are available in our other SDKs.
# Blobs and Trees
Design and construction data is mostly relational: built elements link to each other. Despite this, there is no canonical way of structuring it. How do they relate to each other? Well, it depends!
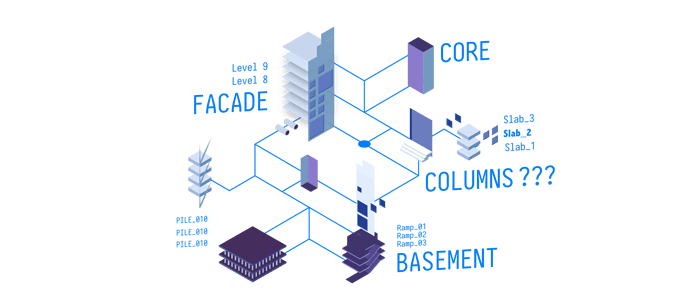
For example, a Site object may contain one or more Building objects. These, in turn, may contain one more Levels, and each of these Levels may contain some Walls, Floor and Beam elements. Or, those Building objects may each individually reference the same Site. Within the Building object, there's all the Walls and Beams, and each of them, rather than being grouped under a Level, they individually reference a specific Level.
In order to solve this, we've taken a good look at how git, the ubiquitous version control system, works. Git operates with two object types: blobs and trees. Blobs represent files, and an important characteristic is that they are immutable - just like objects are in Speckle. Trees represent folders, and they are used to track the hierarchy of the folder structure of your repository.
TIP
If you think this analogy hints to more, you're right: Speckle is becoming a fully fledged version control system for design data. Keep an eye out 😎
As opposed to Git, that deals with data structured on your hard drive, Speckle deals with data structured in memory. In Speckle, an object is, at the same time, both a blob (data) and a tree (its subcomponents). There are two separate, yet interweaved, problems (and their corollaries) that I'll now address:
- How to decompose an object? (Corollary: how to recompose an object?)
- How to serialise, transport and store that decomposed object? (Corollary: how to retrieve and deserialise an object?)
# Decomposing
There is no right or wrong way to structure design data. Different applications operate with different models, different use-cases require different hierarchies, different disciplines and professionals operate with differently structured ontologies.
Speckle now has a mechanism by which, in the process of specifying an object - either via a strongly typed kit, or via dynamic properties - developers (and end-users) can decide what gets decomposed and what doesn't.
# Strongly Typed Detachment
It works, in the case of strongly typed properties, by adding the Speckle specific attribute [DetachProperty] on the properties you want to store as references, rather than within the object itself.
For example, let's take an imaginary set of classes:
public class Building : Base {
[DetachProperty] // this attribute tells Speckle to store the value of the Site separately.
public Site Site { get; set; }
public List<Level> Levels { get; set; }
public Owner { get; set; }
}
public class Level : Base {
public double height { get; set; } = 3.2;
public double baseElevation {get; set; } = 0;
[DetachProperty]
public List<Base> Elements { get; set; } // The actual walls, floors, columns, etc.
}
// Define a site globally
var mySite = new Site();
// Reference the same site in both buildings.
buildingA.Site = mySite;
buildingB.Site = mySite;
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
When an instance of the Building class gets saved, the Site will be stored separately. If two Buildings share the same Site, it will be stored only once, and each instance of the Building class will hold a reference to the same Site.
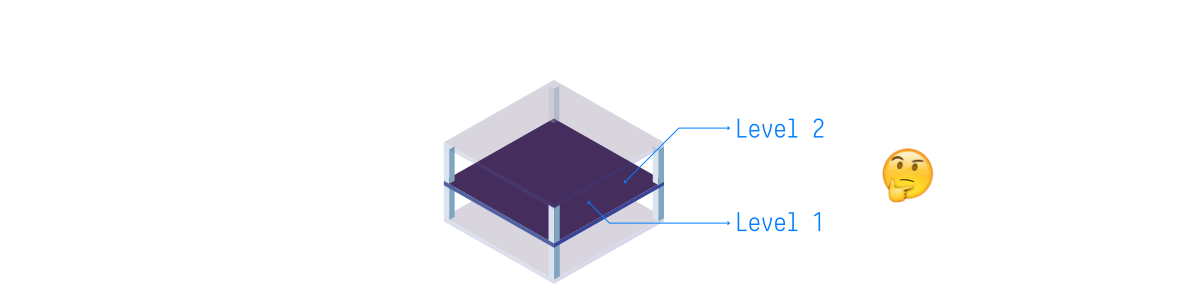
In our example, each Level can hold, in a detachable property, all its walls, beams, ducts, pipes, furniture, and other built elements. Consequently, each of these elements will be individually accessible from the storage layer, and will maintain topological unity. Why is this important? Let's imagine a building with a series of levels separated by floor slabs. The slab between two levels pertains to which level: the bottom one, or the top one?
Collections
The most generic class used in Speckle is the Collection class. The Collection class is a Base class that has the elements property, which is a List<Base>. This means that any object that inherits from Base can be stored in a Collection object. This is a very powerful concept, as it allows us to store arbitrary data structures in Speckle, without paying any penalties. While it is mostly used for representing parent-child relationships, those children can be of any type, and because elements is detached they can also be stored in multiple collections.
# Dynamic Detachment
Let's illustrate this through an example that also demonstrates how dynamically added properties can be detached. We'll assume that we will dynamically set topSlab and bottomSlab properties to each level in our imaginary object model:
// We're grossly simplifying in this example. Here are our two building levels:
var level_1, level_2;
// The philosophical slab instance. Does it belong to level 1 or level 2?
var slab_between_1_and_2 = new Slab();
// Well, it belongs to both! Notice the "@" character at the beginning of
// the dynamic property assignment - it's the Speckle convention for "detaching"
// dynamically added properties.
level_1["@topSlab"] = slab_between_1_and_2;
level_2["@bottomSlab"] = slab_between_1_and_2;
2
3
4
5
6
7
8
9
10
11
Because we've prepended the property name with an "@" symbol, Speckle will now "detach" it. Consequently, once stored, both level one and two will now hold a reference to a single slab! Beyond storage efficiency - the slab is only stored once - this approach gives us the freedom to structure data however is best and, simultaneously, query, slice and dice it however we need to.
For example, let's assume you need to do a quantity takeoffs:
- For each each individual level: specify the total surface area, including walls, ceilings, etc. Solution: simply retrieve each level individually!
- For the whole building: calculate the total volume of concrete that goes into the slabs. Solution: just query the building object for all the slabs!
Similarly, imagine you've written a script that does environmental analysis on a given level. The level can now be retrieved in its entirety - without juggling around to bring in the level above it too, just to get the ceiling out. Once the results are calculated, they can be stored in a detachable property on that specific level (e.g., level_1[@"solarComfortMeshWithColours"] = analysisResultMesh;). Later down the line in your workflow, one can could query for all the "solarComfortMeshWithColours" objects individually for each level, or, if needed, for the whole building.
# Recomposing
Recomposition of an object happens within the deserialisation process, and it's tightly integrated with the transport layer. The process, on the surface, is deceivingly simple. When you ask Speckle to receive a specific object, the process is as follows:
- Speckle retrieves said object's "blob" (actually a JSON string representation of it),
- Next up, Speckle retrieves at all the reference tree of this object,
- Speckle proceeds to deserialise and re-compose the parent object, inserting in the place of references the actual referenced object.
Wether or not this sounds complicated, the exposed API is actually rather simple and the end result is that a decomposed object, when received back, will be identical with the original one - with all its parts in place 💥
# Chunking
# Problem
Some list properties of various objects can get very large. Examples:
- a Brep with many faces will have a Surfaces list prop containing 1000s of potentially heavy Surfaces.
- a mesh with 100k+ vertices and faces.
This results in a clunky (memory heavy) serialisation process and can be unsafe (read: cause breakages) due to memory limitations.
# Solutions
In order of preference. Note that they are not exclusive, and they build on top of each other:
- First, optimise the list property so it's more lightweight
- Second, chunk the list property
# First Port of Call: Optimise the List Property 🧪
For example, you might be tempted to define a mesh like this:
public class Mesh : Base
{
public List<Point> vertices { get; set; }
// ...
}
2
3
4
5
A much more efficient way is to define it like this:
public class Mesh : Base
{
// Typed array of 3
public List<double> vertices { get; set; }
// ...
}
2
3
4
5
6
Instead of storing each individual vertex as a point, you store them in a typed array. Serialisation will be much faster and leaner.
# Second Port of Call: Use the Chunkable Attribute 🆕
In some cases you might be too lazy to actually optimise the storage of a list property, or it might be too convenient to use the class itself.
Alternatively, you might still have a simple List<double> that expands to millions+ of items, like in the case of a very large mesh.
In the cases above, the best way is to mark the property as Chunkable together with [DetachProperty]. This will tell the serialiser that it should split it into manageable chunks of items, the size of which you can control.
Here's how that looks like currently in the mesh class:
public class Mesh : Base
{
[DetachProperty]
[Chunkable(20000)] // Chunks this array into batches of 20k numbers
public List<double> vertices { get; set; } = new List<double>();
[DetachProperty]
[Chunkable(20000)] // Chunks this array into batches of 20k numbers
public List<int> faces { get; set; } = new List<int>();
[DetachProperty]
[Chunkable(20000)] // Chunks this array into batches of 20k numbers
public List<int> colors { get; set; } = new List<int>();
[DetachProperty]
[Chunkable(20000)] // Chunks this array into batches of 20k numbers
public List<double> textureCoordinates { get; set; } = new List<double>();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Potential Footguns
The DetachProperty attribute by itself can be a performance footgun in some scenarios: for example, if you have a List<Point> that can grow really big and you mark it as detachable, without marking it as chunkable, each individual point in that list will be stored as a separate entity.
This is bad: serialisation and deserialisation will take longer, and it essentially amounts to bad object model design (in speckle terms of course).
# Summary
End users and developers can now productively control the way they structure their design data through the decomposition mechanism. From the point of view of the future Speckle connectors, this will enable us to expose object model flexibility in a more elegant way than before to end users. As developers, Speckle gives you another powerful API on top of which you can scaffold your digital automation workflows.
More importantly, this allows you to store arbitrary data structures (scaffolded on top of a Base) with Speckle, without paying any penalties: Speckle deals equally well with flat and nested data.
